第一章:数的认识
1.1 有理数的概念
有理数包括整数和分数。
整数分为正整数、负整数和零。
分数分为正分数和负分数。
1.2 有理数的分类

正有理数:大于零的整数和分数。
负有理数:小于零的整数和分数。
零:既不是正数也不是负数。

1.3 有理数的运算
加法:正数加正数得正数,负数加负数得负数,正数加负数或负数加正数看绝对值大的数的符号。
减法:减去一个数等于加上这个数的相反数。
乘法:同号得正,异号得负,零乘任何数得零。
除法:除以一个数等于乘以这个数的倒数,零不能做除数。
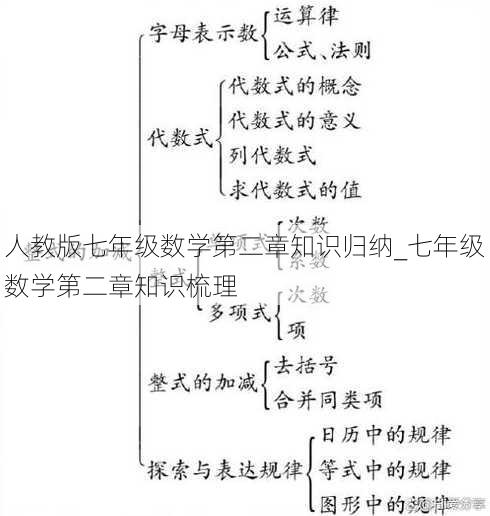
第二章:代数式
2.1 代数式的概念
代数式是由数字、字母和运算符号组成的表达式。
字母代表未知数或变量。
2.2 代数式的分类
简单代数式:只有一个字母或数字的代数式。
复合代数式:由多个简单代数式通过加减乘除等运算组合而成的代数式。
2.3 代数式的运算
合并同类项:将代数式中相同的项合并。
分配律:乘法对加法或减法的分配。
提公因式法:将代数式中的公因式提取出来。
第三章:方程与不等式
3.1 方程的概念
方程是含有未知数的等式。
方程的解是使等式成立的未知数的值。
3.2 一元一次方程
形式:ax + b 0,其中a和b是常数,a ≠ 0。
解法:移项、合并同类项、系数化为1。
3.3 不等式的概念
不等式是表示两个数之间大小关系的式子。
不等式的解集是使不等式成立的数的集合。
3.4 一元一次不等式
形式:ax + b > 0,ax + b < 0,ax + b ≥ 0,ax + b ≤ 0。
解法:移项、合并同类项、系数化为1。
常见问题及回答
- 问:有理数和整数有什么区别?
答: 有理数包括整数和分数,而整数是有理数的一部分,整数是没有小数部分的数。
- 问:如何解一元一次方程?
答: 解一元一次方程的步骤是:移项、合并同类项、系数化为1。
- 问:代数式中的字母可以代表什么?
答: 字母可以代表未知数、已知数或者任何具体的数值。
- 问:如何合并同类项?
答: 合并同类项是将代数式中相同的项的系数相加或相减。
- 问:一元一次不等式的解集是什么?
答: 一元一次不等式的解集是使不等式成立的数的集合,通常用区间表示。
- 问:如何判断两个代数式是否是同类项?
答: 两个代数式是同类项的条件是:它们所含的字母相同,并且相同字母的指数也相同。
