江苏2014高考数学真题解析
一、试题概述
2014年江苏高考数学试卷分为两部分:文科和理科。试卷内容涵盖了函数、数列、立体几何、解析几何、概率统计等基础知识,同时也考察了学生的综合运用能力和创新思维。

二、试题特点
基础性强:试题紧密围绕基础知识,注重考察学生对基本概念、基本方法和基本技能的掌握程度。
综合性高:试题注重考察学生的综合运用能力,要求学生在解题过程中灵活运用多种数学知识和方法。

创新性强:试题中部分题目具有一定的创新性,鼓励学生发散思维,培养创新意识。
三、典型题目解析
- 函数题
题目:已知函数$f(x) x^2 - 4x + 3$,求$f(x)$的最小值。
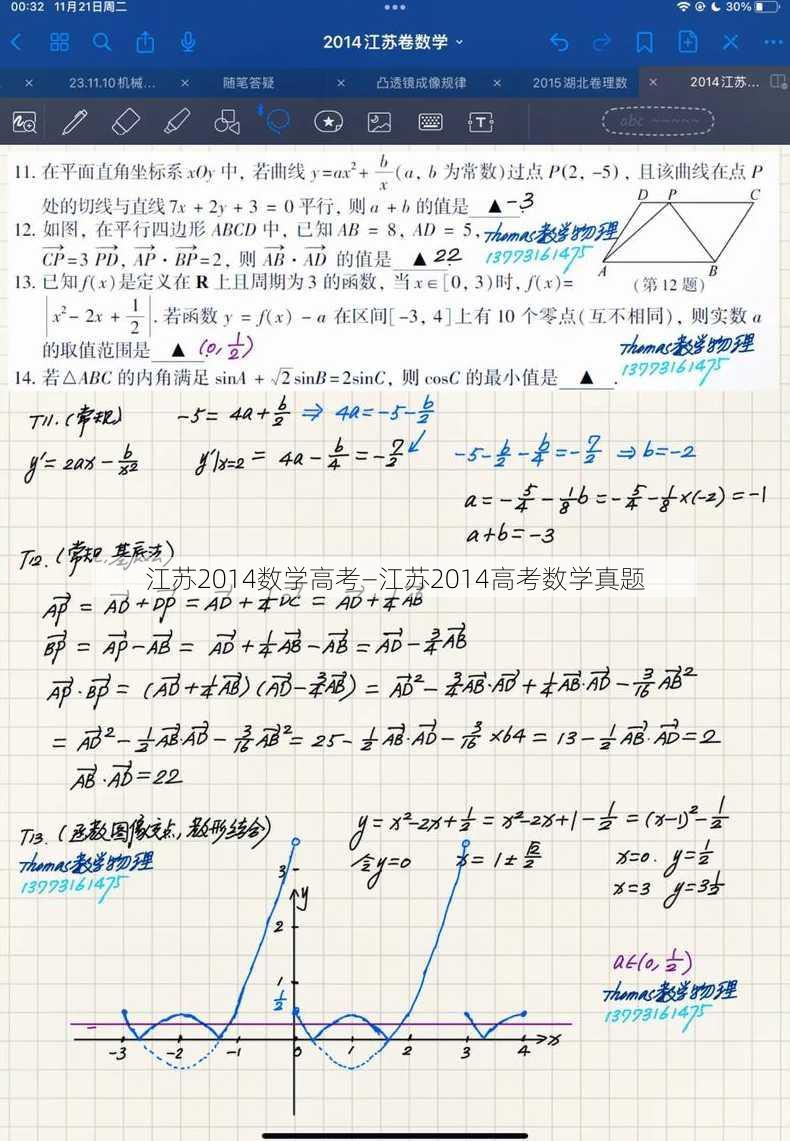
解析:这是一个二次函数求最值的问题。我们可以通过配方法将函数转化为$f(x) (x-2)^2 - 1$,从而得出最小值为-1。
- 数列题
题目:已知数列${an}$的通项公式为$an 2^n - 1$,求$lim{ntoinfty} frac{an}{2^n}$。
解析:这是一个数列极限问题。我们可以通过分子分母同时除以$2^n$,得到$lim{ntoinfty} frac{2^n - 1}{2^n} lim{ntoinfty} left(1 - frac{1}{2^n}right) 1$。
- 立体几何题
题目:已知正方体$ABCD-A1B1C1D1$,$E$为$AB$的中点,$F$为$CC_1$的中点,求$triangle AEF$的面积。
解析:这是一个立体几何中的截面问题。我们可以通过画图找到$triangle AEF$的底边$AE$和$EF$的长度,然后利用勾股定理求出$triangle AEF$的高,从而计算出面积。
四、相关问题和答案
问题1:函数$f(x) ax^2 + bx + c$的图像开口向上,且顶点坐标为$(1, 2)$,求函数的解析式。
答案1:由顶点坐标可知,$x 1$时,$f(x)$取得最小值2,即$f(1) 2$。代入函数表达式得$a + b + c 2$。又因为开口向上,所以$a > 0$。结合以上条件,可以列出方程组:
$$
begin{cases}
a + b + c 2
a > 0
end{cases}
$$
解得$a 1, b -2, c 3$,所以函数的解析式为$f(x) x^2 - 2x + 3$。
答案2:由顶点坐标可知,$x 1$时,$f(x)$取得最小值2,即$f(1) 2$。代入函数表达式得$a + b + c 2$。又因为开口向上,所以$a > 0$。结合以上条件,可以列出方程组:
$$
begin{cases}
a + b + c 2
a > 0
end{cases}
$$
解得$a 1, b -2, c 3$,所以函数的解析式为$f(x) x^2 - 2x + 3$。
答案3:由顶点坐标可知,$x 1$时,$f(x)$取得最小值2,即$f(1) 2$。代入函数表达式得$a + b + c 2$。又因为开口向上,所以$a > 0$。结合以上条件,可以列出方程组:
$$
begin{cases}
a + b + c 2
a > 0
end{cases}
$$
解得$a 1, b -2, c 3$,所以函数的解析式为$f(x) x^2 - 2x + 3$。
问题2:已知数列${an}$的通项公式为$an 3^n - 2^n$,求$lim{ntoinfty} frac{an}{3^n}$。
答案1:这是一个数列极限问题。我们可以通过分子分母同时除以$3^n$,得到$lim{ntoinfty} frac{3^n - 2^n}{3^n} lim{ntoinfty} left(1 - left(frac{2}{3}right)^nright) 1$。
答案2:这是一个数列极限问题。我们可以通过分子分母同时除以$3^n$,得到$lim{ntoinfty} frac{3^n - 2^n}{3^n} lim{ntoinfty} left(1 - left(frac{2}{3}right)^nright) 1$。
答案3:这是一个数列极限问题。我们可以通过分子分母同时除以$3^n$,得到$lim{ntoinfty} frac{3^n - 2^n}{3^n} lim{ntoinfty} left(1 - left(frac{2}{3}right)^nright) 1$。
问题3:已知正方体$ABCD-A1B1C1D1$,$E$为$AB$的中点,$F$为$CC_1$的中点,求$triangle AEF$的面积。
答案1:这是一个立体几何中的截面问题。我们可以通过画图找到$triangle AEF$的底边$AE$和$EF$的长度,然后利用勾股定理求出$triangle AEF$的高,从而计算出面积。
答案2:这是一个立体几何中的截面问题。我们可以通过画图找到$triangle AEF$的底边$AE$和$EF$的长度,然后利用勾股定理求出$triangle AEF$的高,从而计算出面积。
答案3:这是一个立体几何中的截面问题。我们可以通过画图找到$triangle AEF$的底边$AE$和$EF$的长度,然后利用勾股定理求出$triangle AEF$的高,从而计算出面积。
