高考双曲线是什么

高考双曲线概述

1. 定义

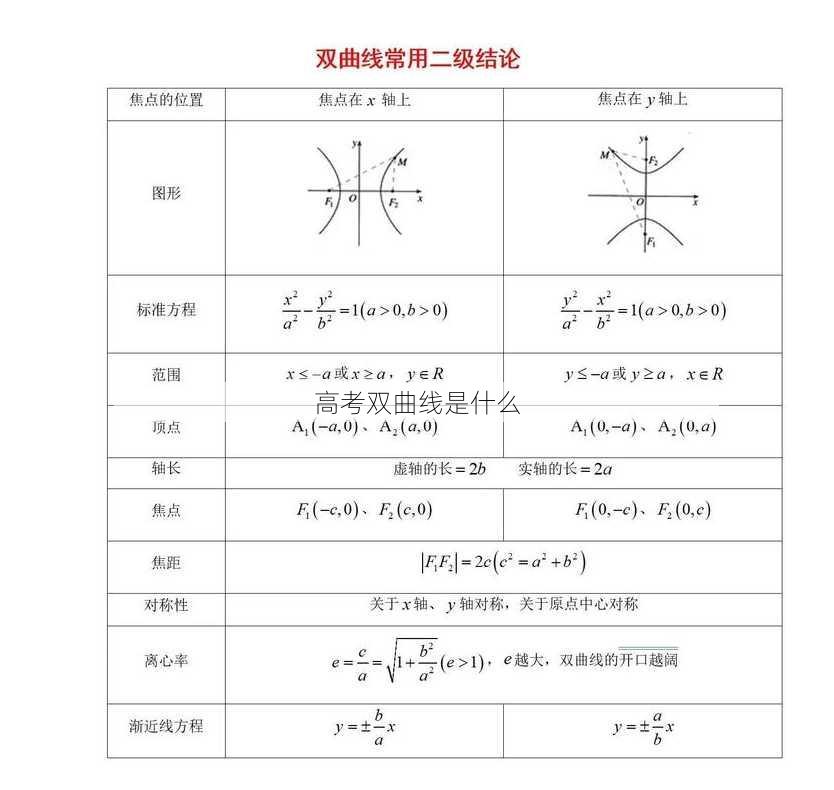
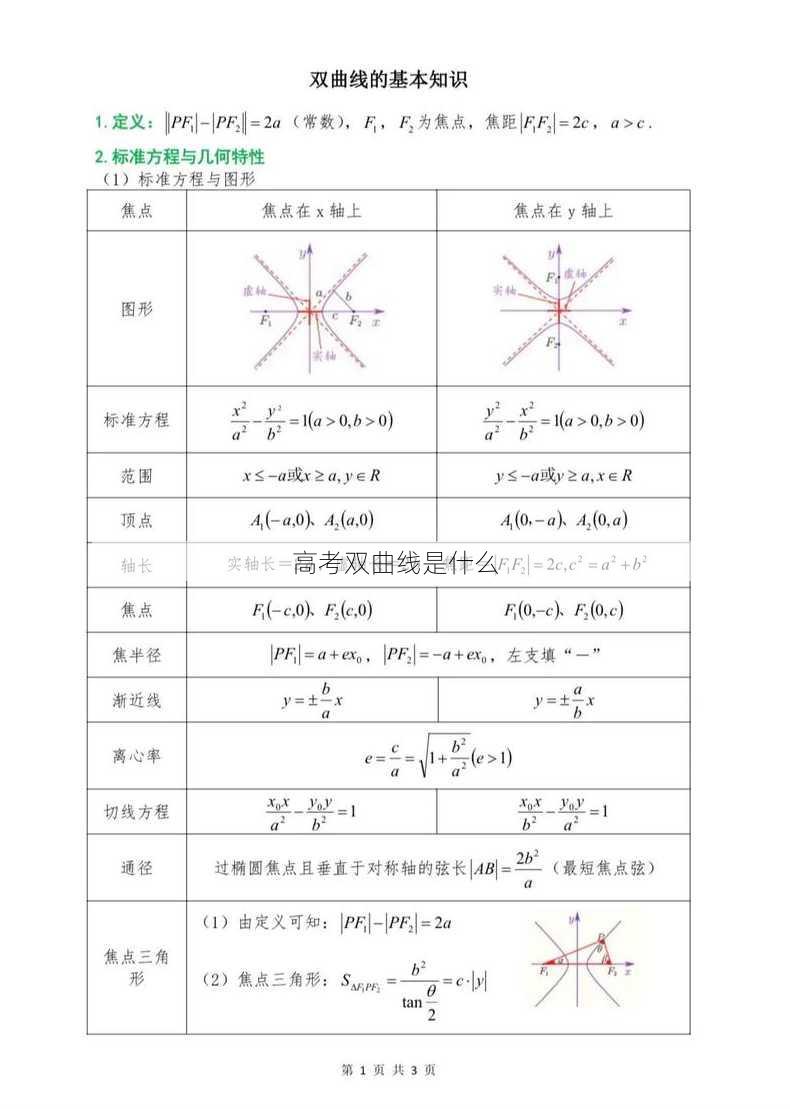
高考双曲线是指在高考数学考试中，涉及到的关于双曲线的相关知识。双曲线是一种圆锥曲线，其方程为 ( frac{x^2}{a^2} - frac{y^2}{b^2} 1 )（( a > 0, b > 0 )），其中 ( a ) 和 ( b ) 是双曲线的两个重要参数。

2. 标准方程

双曲线的标准方程如上所述，其中 ( a ) 是实轴的半长，( b ) 是虚轴的半长。双曲线有两个渐近线，方程为 ( y pm frac{b}{a}x )。

3. 几何性质

• 焦点：双曲线的两个焦点位于实轴上，距离原点 ( c ) 的距离，其中 ( c^2 a^2 + b^2 )。

• 顶点：双曲线的顶点位于实轴上，距离原点 ( a ) 的距离。

• 渐近线：双曲线的渐近线是直线 ( y pm frac{b}{a}x )，随着 ( x ) 的增大或减小，曲线趋近于这些直线。

  

4. 应用

双曲线在物理学、工程学、天文学等领域有广泛的应用，如光学中的透镜设计、电子学中的电路设计等。

常见问题及回答

1. 问题：双曲线的焦点和顶点有什么区别？

回答：双曲线的焦点位于实轴上，距离原点 ( c ) 的距离，其中 ( c^2 a^2 + b^2 )；而顶点位于实轴上，距离原点 ( a ) 的距离。焦点是双曲线的特殊点，对于双曲线的性质有重要影响。

2. 问题：双曲线的渐近线方程是什么？

回答：双曲线的渐近线方程是 ( y pm frac{b}{a}x )。当 ( x ) 趋向于正无穷或负无穷时，双曲线的图形会趋近于这两条直线。

3. 问题：双曲线的离心率是多少？

回答：双曲线的离心率 ( e ) 是一个无理数，定义为 ( e frac{c}{a} )，其中 ( c ) 是焦点到原点的距离，( a ) 是实轴的半长。离心率 ( e ) 的值总是大于 1。