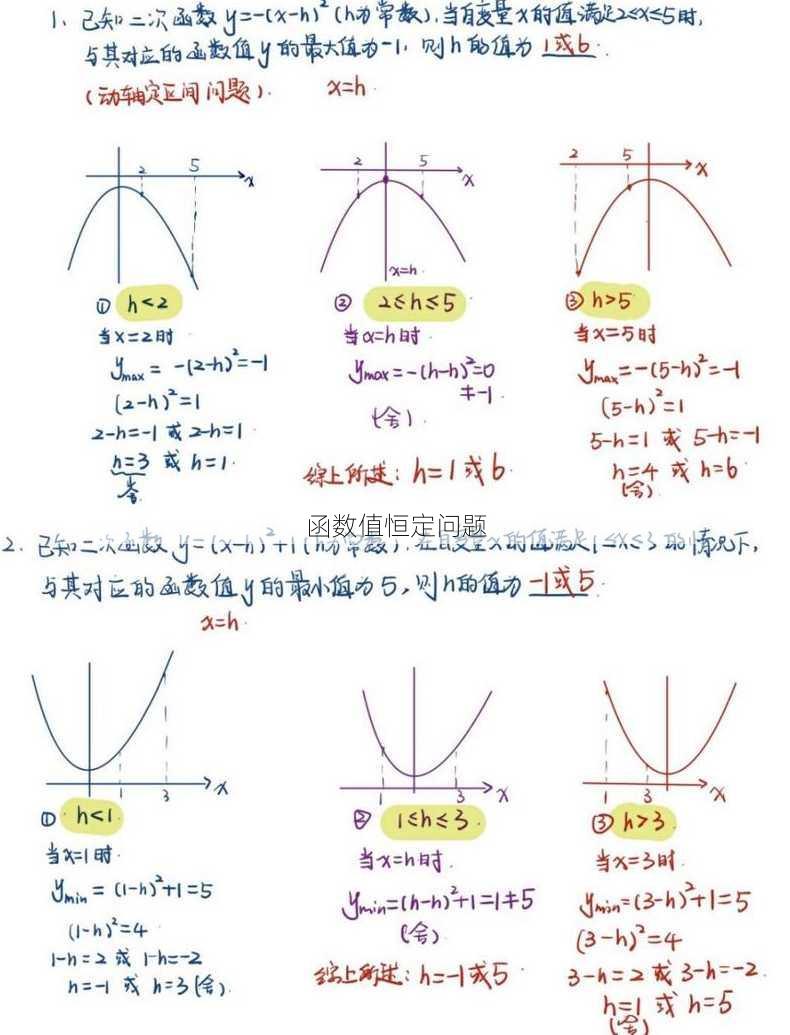
函数值恒定问题概述
函数值恒定问题,指的是在某些条件下,函数的值始终保持不变的情况。这类问题在数学、物理、工程等多个领域都有广泛的应用。本文将深入探讨函数值恒定的概念、性质以及应用。
一、函数值恒定的定义

函数值恒定,即对于函数 ( f(x) ),存在某个常数 ( C ),使得对于定义域内的所有 ( x ),都有 ( f(x) C )。换句话说,函数的值在整个定义域内都是相同的。
二、函数值恒定的性质
单调性:如果函数 ( f(x) ) 在定义域内是单调的,那么函数值恒定。
连续性:如果函数 ( f(x) ) 在定义域内是连续的,那么函数值恒定。
可导性:如果函数 ( f(x) ) 在定义域内是可导的,那么函数值恒定。
三、函数值恒定的应用

数学分析:在数学分析中,函数值恒定是证明某些数学定理的重要工具。
物理学:在物理学中,函数值恒定可以用来描述某些物理量的不变性。
工程学:在工程学中,函数值恒定可以用来分析某些工程问题的稳定性。
函数值恒定问题的实例分析
实例一:常函数
常函数 ( f(x) C ) 是函数值恒定的典型例子。在定义域内,无论 ( x ) 取何值,函数值都为常数 ( C )。
实例二:指数函数
指数函数 ( f(x) e^x ) 在定义域内是单调递增的,因此不是函数值恒定的例子。
实例三:对数函数
对数函数 ( f(x) ln x ) 在定义域内是单调递增的,因此不是函数值恒定的例子。
常见问题及回答
问题一:函数值恒定与函数单调性有何关系?
回答: 函数值恒定与函数单调性有密切关系。如果函数在定义域内是单调的,那么函数值恒定;反之,如果函数值恒定,那么函数在定义域内是单调的。
问题二:函数值恒定与函数连续性有何关系?
回答: 函数值恒定与函数连续性有密切关系。如果函数在定义域内是连续的,那么函数值恒定;反之,如果函数值恒定,那么函数在定义域内是连续的。
问题三:函数值恒定与函数可导性有何关系?
回答: 函数值恒定与函数可导性有密切关系。如果函数在定义域内是可导的,那么函数值恒定;反之,如果函数值恒定,那么函数在定义域内是可导的。
