t检验是计量经济学中常用的统计检验方法之一,用于检验两个或多个样本均值之间是否存在显著差异。本文将详细介绍t检验的基本原理、类型、计算方法和应用场景。
t检验的基本原理
t检验基于以下假设:

正态分布:样本数据服从正态分布。
同方差性:不同样本之间的方差相等。
当这些假设成立时,t检验可以有效地检验样本均值之间的差异是否显著。
t检验的类型
单样本t检验:用于检验单个样本的均值是否与总体均值相等。
双样本t检验:用于比较两个独立样本的均值是否存在显著差异。
配对样本t检验:用于比较两个相关样本的均值是否存在显著差异。
t检验的计算方法
- 计算t统计量:t统计量是衡量样本均值差异的指标,计算公式如下:
```
t (x̄ - μ) / (s / √n)
```
其中,x̄为样本均值,μ为总体均值,s为样本标准差,n为样本容量。
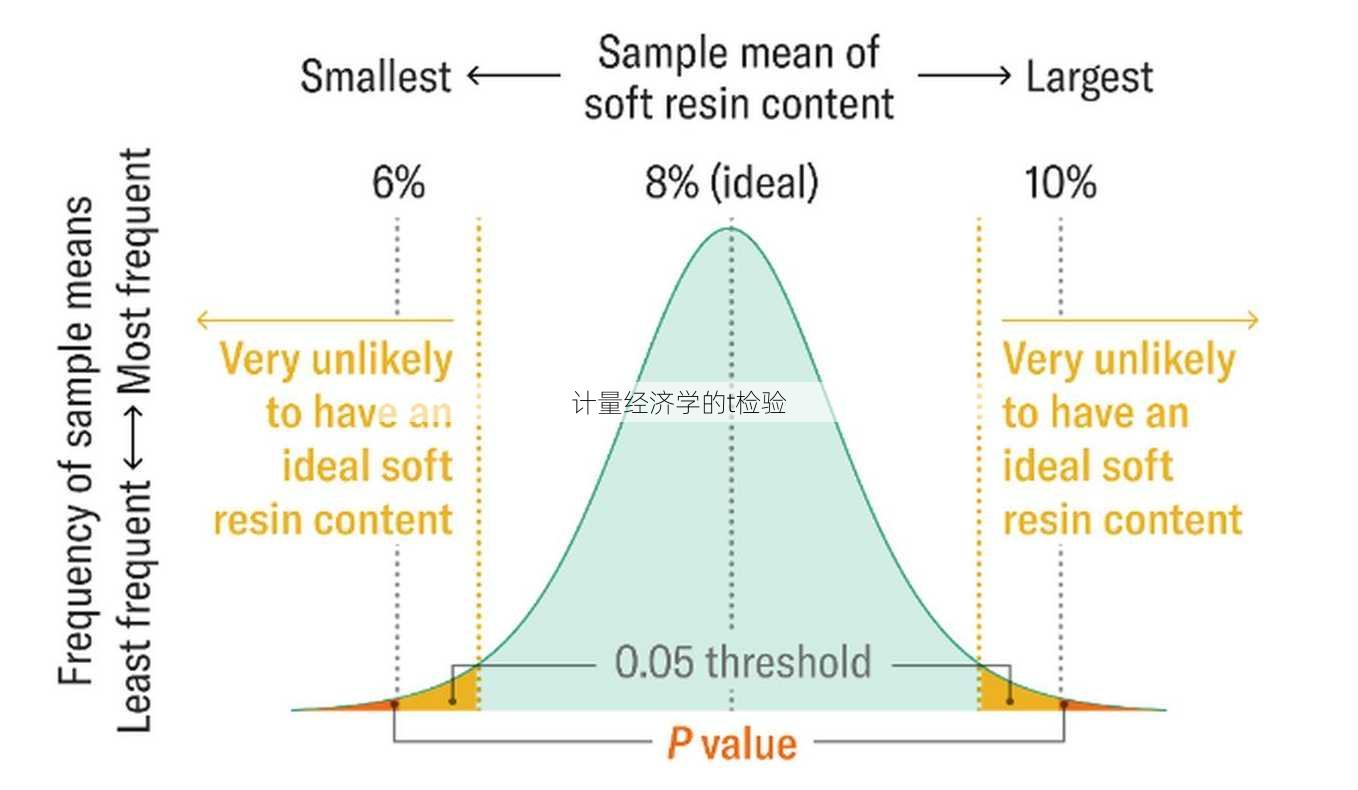
确定临界值:根据自由度和显著性水平,从t分布表中查找临界值。
比较t统计量和临界值:如果t统计量大于临界值,则拒绝原假设,认为样本均值之间存在显著差异。
t检验的应用场景
假设检验:检验样本数据是否符合某个特定的假设。
比较不同组别:比较不同组别之间的均值是否存在显著差异。
模型诊断:用于检验计量经济学模型的假设条件。
t检验是一种重要的统计检验方法,在计量经济学中应用广泛。掌握t检验的基本原理、类型、计算方法和应用场景对于进行有效的统计分析具有重要意义。
相关问题及回答
问题1:t检验适用于哪些类型的数据?
回答:t检验适用于连续型数据,且数据应服从正态分布。
问题2:t检验与Z检验有什么区别?
回答:t检验和Z检验都是用于检验样本均值是否与总体均值相等,但t检验适用于样本容量较小或总体标准差未知的情况,而Z检验适用于样本容量较大或总体标准差已知的情况。
问题3:如何判断t检验结果的可靠性?
回答:可以通过以下方法判断t检验结果的可靠性:检查数据是否符合正态分布和同方差性假设;比较t统计量与临界值;考虑显著性水平。
